Current Division and Voltage Division Rule

Current Division Rule

A parallel circuit functions as a current divider, where the incoming current splits among all branches while the voltage across each branch remains constant. The Current Division Rule is used to determine the current through circuit impedances, as illustrated by the circuit below:

The current $I$ splits into $I 1$ and $I 2$ across two parallel branches with resistances $R 1$ and $R 2$ , where $V$ denotes the voltage drop across both resistances. As is known,

Then the equation of the current is written as:

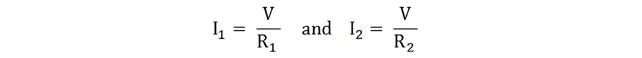
Let the total resistance of the circuit be R and is given by the equation shown below:

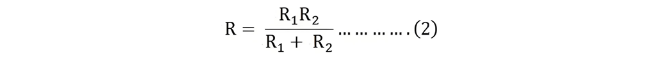
Equation (1) can also be written as:

Now, putting the value of R from the equation (2) in the equation (3) we will get

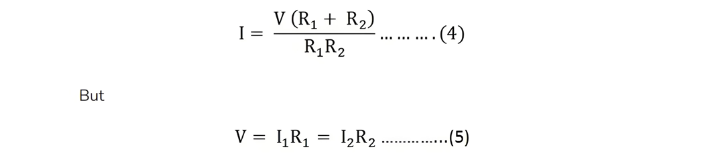
Putting the value of V = I₁R₁ from the equation (5) in equation (4), we finally get the equation as:

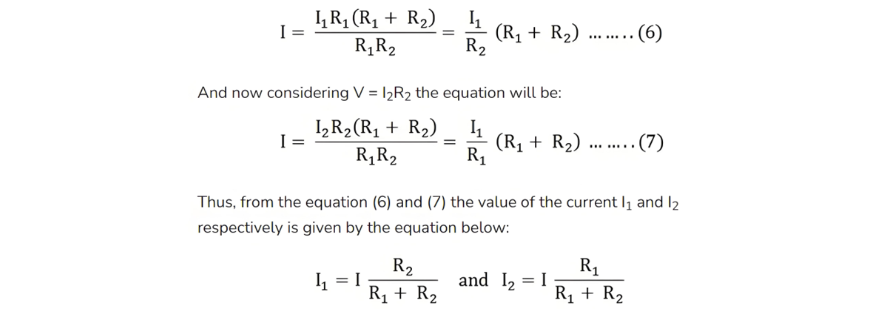
Thus, the Current Division Rule states that the current in any parallel branch equals the ratio of the opposite branch resistance to the total resistance, multiplied by the total current.
Voltage Division Rule
The Voltage Division Rule can be understood by examining the series circuit below. In a series circuit, voltage is divided, while the current remains constant.

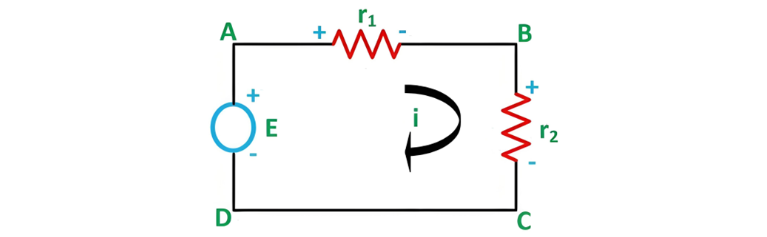
Let us consider a voltage source E with the resistance r₁and r₂ connected in series across it.

As we know,

I = V/R or we can say I = E/R

Therefore, the current (i) in the loop ABCD will be:

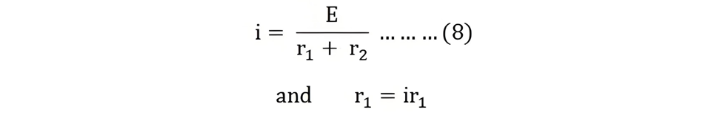
Thus, the voltage across a resistor in a series circuit is equal to the product of the resistor's value, the total impressed voltage across the series elements, and the reciprocal of the total resistance of the series elements.