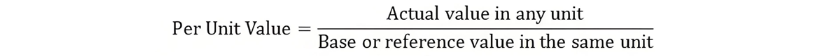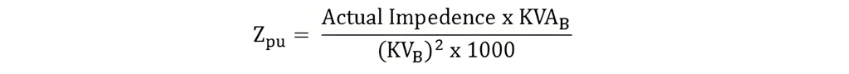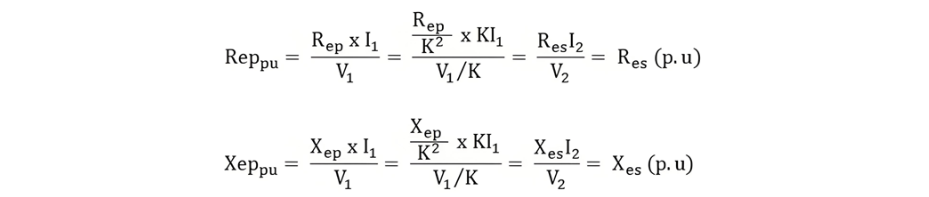Per-Unit System in Electrical Machine Analysis
For the analysis of electrical machines or their systems, diverse parameter values are often required. The per-unit (pu) system provides standardized representations for voltage, current, power, impedance, and admittance, streamlining calculations by normalizing all values to a common base. This system is particularly advantageous in circuits with fluctuating voltages, where it simplifies cross-referencing and analysis.
Definition
The per-unit value of a quantity is defined as the ratio of its actual value (in any unit) to a chosen base or reference value (in the same unit). Mathematically, any quantity is converted to its per-unit form by dividing its numerical value by the corresponding base value of the same dimension. Notably, per-unit values are dimensionless, eliminating unit dependencies and facilitating uniform analysis across different systems.
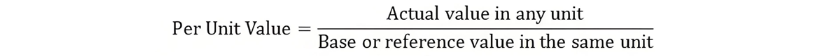

Putting the value of base current from the equation (1) in the equation (3) we get

Putting the value of base impedance from the equation (4) in the equation (5) we will get the value of impedance per unit
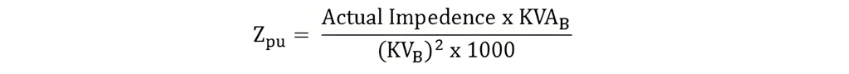
Advantages of Per-Unit System
The per-unit system offers two primary advantages in electrical engineering analysis:
-
Standardized Parameter Representation When expressed in per-unit terms, the parameters of rotating electrical machines and transformers (e.g., resistance, reactance, impedance) fall within consistent numerical ranges, regardless of their specific ratings. This standardization enables intuitive comparisons between devices of different sizes or voltage classes, streamlining design and analysis workflows.
-
Elimination of Transformer Side Referencing The per-unit system removes the need to reference circuit quantities to the primary or secondary side of a transformer. By normalizing all parameters to a common base, it simplifies calculations by eliminating the complexity of cross-side conversions. For instance, if a transformer has a per-unit resistance Rpu and reactance Xpu referred to the primary, these values remain consistent and require no further adjustment for secondary-side analysis.
This approach significantly reduces computational overhead in power system studies, making it an indispensable tool for analyzing complex networks involving multiple transformers and machines.

Where Rep and Xep denote the resistance and reactance referred to the primary side, with "pu" signifying the per-unit system.
The per-unit values of resistance and leakage reactance referred to the primary side are identical to those referred to the secondary side because the per-unit system inherently normalizes parameters using base values, eliminating the need for side-specific referencing. This equivalence arises from the consistent scaling of all quantities (voltage, current, impedance) to a common base, ensuring that per-unit parameters remain invariant across transformer side
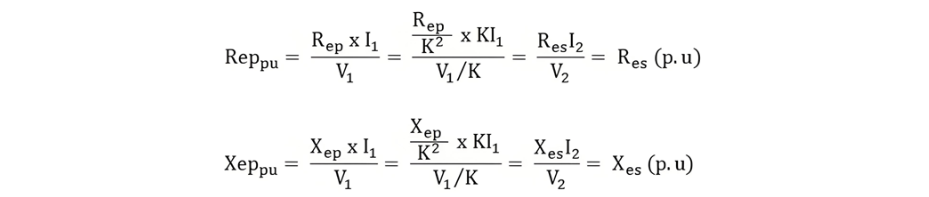
Where Res and Xes represent the equivalent resistance and reactance referred to the secondary side.
Thus, it can be inferred from the above two equations that the ideal transformer component can be eliminated. This is because the per-unit impedance of the transformer's equivalent circuit remains identical whether calculated from the primary or secondary side, provided that the voltage bases on both sides are chosen in the ratio of the transformation ratio. This invariance arises from the consistent normalization of electrical quantities, ensuring that the per-unit representation inherently accounts for the transformer's turns ratio without requiring explicit ideal transformer modeling.