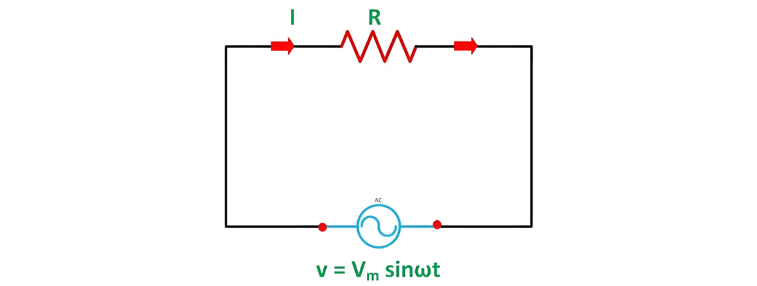
Pure Resistive AC Circuit
A circuit containing only a pure resistance R (in ohms) in an AC system is defined as a Pure Resistive AC Circuit, devoid of inductance and capacitance. Alternating current and voltage in such a circuit oscillate bidirectionally, generating a sine wave (sinusoidal waveform). In this configuration, power is dissipated by the resistor, with voltage and current in perfect phase—both reaching their peak values simultaneously. As a passive component, the resistor neither generates nor consumes electric power; instead, it converts electrical energy into heat.
Explanation of Resistive Circuit
In an AC circuit, the voltage-to-current ratio is influenced by supply frequency, phase angle, and phase difference. Notably, in an AC resistive circuit, the resistance value remains constant regardless of the supply frequency.
Consider an alternating voltage applied across the circuit, described by the equation:
Then the instantaneous value of current flowing through the resistor shown in the figure below will be:
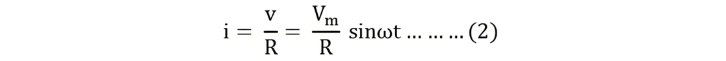
The value of current will be maximum when ωt= 90° or sinωt = 1.Putting the value of sinωt in equation (2) we will get
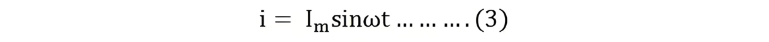
Phase Angle and Waveform in Resistive Circuit
From Equations (1) and (3), it is evident that no phase difference exists between the applied voltage and the current in a pure resistive circuit—the phase angle between voltage and current is zero. Consequently, in an AC circuit with pure resistance, the current is in perfect phase with the voltage, as illustrated in the waveform diagram below:
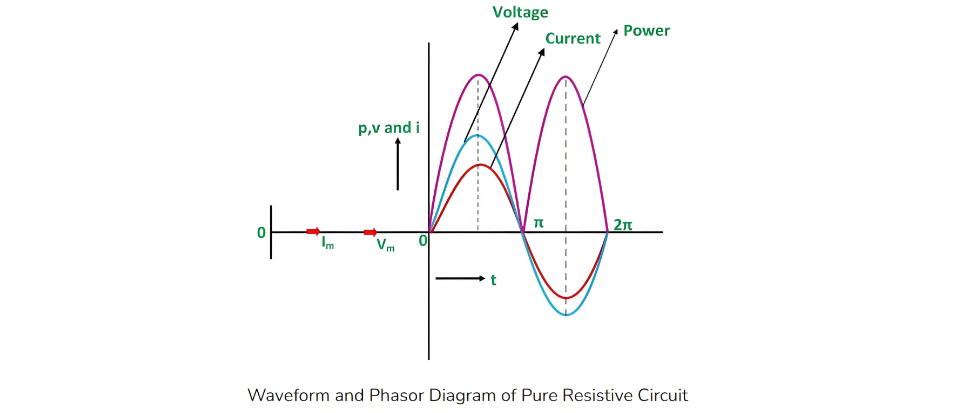
Power in Pure Resistive Circuit
The power curve waveform uses three colors—red, blue, and pink—to represent the current, voltage, and power curves, respectively. The phasor diagram confirms that current and voltage are in phase, meaning their peaks occur simultaneously. As a result, the power curve remains positive for all voltage and current values.
In a DC circuit, power is defined as the product of voltage and current. Similarly, in an AC circuit, power is calculated using the same principle, though it considers the instantaneous values of voltage and current. Thus, the instantaneous power in a pure resistive circuit is expressed by:
Instantaneous power: p = vi
The average power consumed in the circuit over a complete cycle is given by
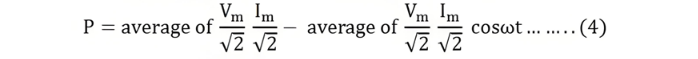
As the valve of cosωt is zero.So, putting the value of cosωt in equation (4) the value of power will be given by
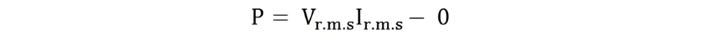
Where,
- P – average power
- Vr.m.s – root mean square value of supply voltage
- Ir.m.s – root mean square value of the current
Hence, the power in a purely resistive circuit is given by:
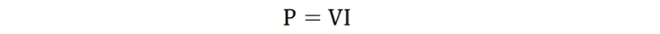
In a pure resistive circuit, voltage and current are in perfect phase with a zero phase angle, meaning no phase difference exists between them. The alternating quantities reach their peak values at the same time intervals, and the rise and fall of voltage and current occur simultaneously.