Why 3-Phase Power? Why Not 6, 12 or More for Power Transmission?

It is well-known that single-phase and three-phase systems are the most prevalent configurations for power transmission, distribution, and end-use applications. While both serve as fundamental power supply frameworks, three-phase systems offer distinct advantages over their single-phase counterparts.

Notably, multi-phase systems (such as 6-phase, 12-phase, etc.) find specific applications in power electronics—particularly in rectifier circuits and variable frequency drives (VFDs)—where they effectively reduce ripple in pulsating DC outputs. Achieving multi-phase configurations (e.g., 6, 9, or 12 phases) historically involved complex phase-shifting techniques or motor-generator sets, but these approaches remain economically infeasible for large-scale power transmission and distribution over extended distances.

Why 3-Phase Instead of 1-Phase Supply System?

The main advantage of three phase over a single phase or two phase system is that we can transmit more (constant and uniform) power.

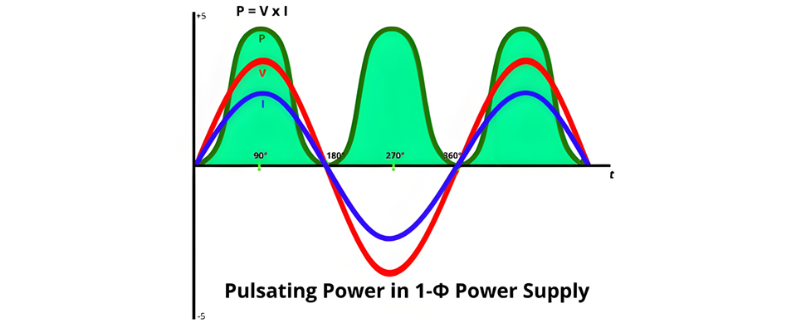
Power in Single Phase System

P = V . I . CosФ

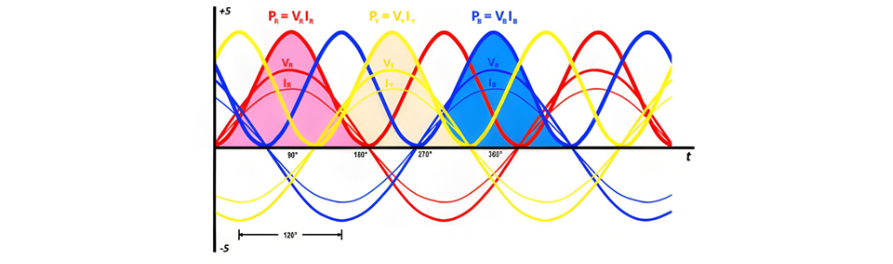
Power in Three Phase System

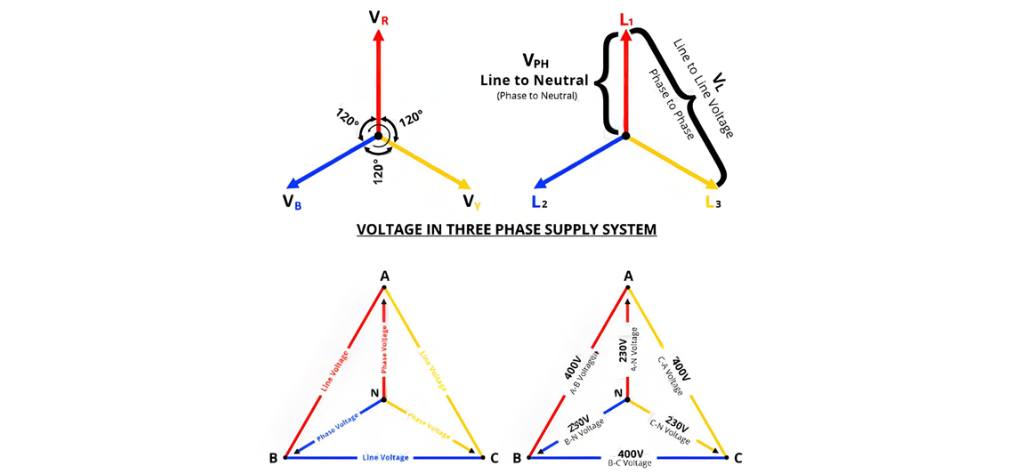
P = √3 . V_L . I_L . CosФ … Or
P = 3 x. V_PH . I_PH . CosФ

Where:

P = Power in Watts
V_L = Line Voltage
I_L = Line Current
V_PH = Phase Voltage
I_PH = Phase Current
CosФ = Power factor

It is evident that the power capacity of a three-phase system is 1.732 (√3) times higher than that of a single-phase system. By comparison, a two-phase supply transmits 1.141 times more power than a single-phase configuration.

A key advantage of three-phase systems is the rotating magnetic field (RMF), which enables self-starting in three-phase motors while ensuring constant instantaneous power and torque. In contrast, single-phase systems lack an RMF and exhibit pulsating power, limiting their performance in motor applications.

Three-phase systems also offer superior transmission efficiency, with reduced power loss and voltage drop. For instance, in a typical resistive circuit:

Single Phase System

Power loss in transmission line = 18I²r … (P = I²R)
Voltage drop in transmission line = I.6r … (V = IR)

Three Phase System

Power loss in transmission line = 9I²r … (P = I²R)
Voltage drop in transmission line = I.3r … (V = IR)

It is shown that the voltage drop and power loss in a three-phase system are 50% lower than those in a single-phase system.

Two-phase supplies, similar to three-phase ones, can provide constant power, generate RMF (rotating magnetic field), and offer constant torque. However, three-phase systems carry more power than two-phase systems due to the extra phase. This raises the question: why not use more phases like 6, 9, 12, 24, 48, etc.? We will discuss this in detail and explain how a three-phase system can transmit more power than a two-phase system with the same number of wires.

Why Not Two-Phase?

Both two-phase and three-phase systems can generate rotating magnetic fields (RMF) and provide constant power and torque, but three-phase systems offer a key advantage: higher power capacity. The extra phase in three-phase setups allows for 1.732 times more power transmission than two-phase systems with the same conductor size.

Two-phase systems typically require four wires (two phase conductors and two neutrals) to complete circuits. Using a common neutral to form a three-wire system reduces wiring, but the neutral must carry combined return currents from both phases—needing thicker conductors (e.g., copper) to avoid overheating. In contrast, three-phase systems use three wires for balanced loads (delta configuration) or four wires for unbalanced loads (star configuration), optimizing power delivery and conductor efficiency.、

Why Not 6-Phase, 9-Phase, or 12-Phase?

While higher-phase systems can reduce transmission losses, they aren’t widely adopted due to practical limitations:

Conductor Efficiency: Three-phase systems use the fewest conductors (3) to transmit balanced power, while a 12-phase system would need 12 conductors—quadrupling material and installation costs.
Harmonic Suppression: The 120° phase angle in three-phase systems naturally cancels third harmonic currents, eliminating the need for complex filters required in higher-phase setups.
System Complexity: Higher-phase systems demand reengineered components (transformers, circuit breakers, switchgear) and larger substations, increasing design complexity and maintenance overhead.
Practical Constraints: Motors and generators with more than three phases are bulkier and harder to cool, while transmission towers would need greater height to accommodate more conductors.

The Three-Phase Advantage

Three-phase systems strike an optimal balance:

They transmit 50% more power than single-phase systems with the same conductors, minimizing losses.
The 120° phase configuration balances loads and suppresses harmonics without added complexity.
They adapt to both delta (balanced loads) and star (unbalanced loads) setups, supporting diverse power needs.

Higher-phase systems offer diminishing returns—each extra phase raises costs exponentially while providing marginal benefits. For this reason, three-phase technology remains the global standard for power transmission, balancing efficiency, simplicity, and economic viability.