Peak Value, Average Value and RMS Value

Definition of Peak Value

The peak value of an alternating quantity refers to the maximum magnitude it reaches within one cycle. Also known as the maximum value, amplitude, or crest value, this parameter for a sinusoidal quantity occurs at 90 degrees, as illustrated in the figure below. Peak values of alternating voltage and current are denoted by

E m

and

I m

, respectively.

Average Value of Alternating Quantities
The average value of an alternating voltage or current is defined as the mean of all instantaneous values over one complete cycle.For symmetrical waveforms like sinusoidal signals, the positive half-cycle mirrors the negative half-cycle. Consequently, the average value over a full cycle is zero due to algebraic cancellation.

Since both half-cycles perform work, the average value is calculated without considering sign conventions. Thus, only the positive half-cycle is used to determine the average value for sinusoidal waveforms. This concept is best illustrated through an example:

Divide the positive half cycle into (n) number of equal parts as shown in the above figure

Let i₁, i₂, i₃…….. i_nbe the mid ordinates

The Average value of current I_av = mean of the mid ordinates

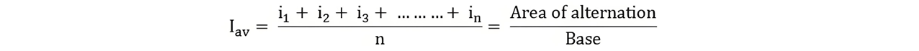
RMS Value Definition and Principle
The RMS (Root Mean Square) value of an alternating current is defined as the steady current that, when passed through a resistor for a specified time, generates the same amount of heat as the alternating current through the same resistor over the same period.

Alternatively, the RMS value is the square root of the mean of the squares of all instantaneous values of the current.

Principle Explanation

Consider an alternating current

I

flowing through a resistor

R

for time

t

, producing the same heat as a direct current I_eff. As illustrated below, the current's cycle is divided into

n

equal intervals of

t/n

seconds each:

Let i₁, i₂, i₃,………..in be the mid ordinates

Then the heat produced in

RMS Value Definition and Significance

Mathematically, the RMS (Root Mean Square) value is expressed as I_eff = square root of mean of squares of instantaneous values . This value quantifies the energy transfer capability of an AC source, distinguishing it as the true measure of an alternating current or voltage's practical effect.

Ammeters and voltmeters inherently record RMS values. For instance, a standard domestic single-phase AC supply rated at 230 V, 50 Hz specifies the RMS voltage, as this value dictates the energy delivered to electrical loads. In DC circuits, voltage and current remain constant, simplifying magnitude evaluation, whereas AC systems require specialized metrics due to their time-varying nature. Alternating quantities are characterized by three key parameters: peak value (the maximum instantaneous magnitude), average value (the mean of positive half-cycle values), and RMS value (the effective DC-equivalent for energy transfer). These metrics collectively enable precise analysis of AC system behavior and power transfer.