Effect of Load on a Synchronous Motor

A synchronous motor operates at a constant synchronous speed, irrespective of the load. Now, let's examine the impact of load variation on the motor. Suppose a synchronous motor is initially running with a leading power factor. The phasor diagram corresponding to the leading power factor is presented as follows:

When the load on the shaft is increased, the rotor experiences a momentary slowdown. This occurs because it takes some time for the motor to draw the additional power from the electrical line. In other words, although the rotor maintains its synchronous rotational speed, it effectively "slips back" in spatial position due to the increased load demand. During this process, the torque angle δ expands, which in turn causes the induced torque to increase.

The equation for the induced torque is expressed as follows:

Subsequently, the increased torque accelerates the rotor, enabling the motor to once again achieve synchronous speed. However, this restoration occurs with a larger torque angle δ. The excitation voltage Ef is directly proportional to ϕω, relying on both the field current and the motor's rotational speed. Given that the motor operates at a constant synchronous speed and the field current remains unchanged, the magnitude of the voltage

|Ef|

stays constant. Therefore, we can conclude that

From the equations above, it becomes evident that when the power P increases, the values of Ef sinδ and Ia cosϕ also rise accordingly.The following figure illustrates the impact of a load increase on the operation of a synchronous motor.

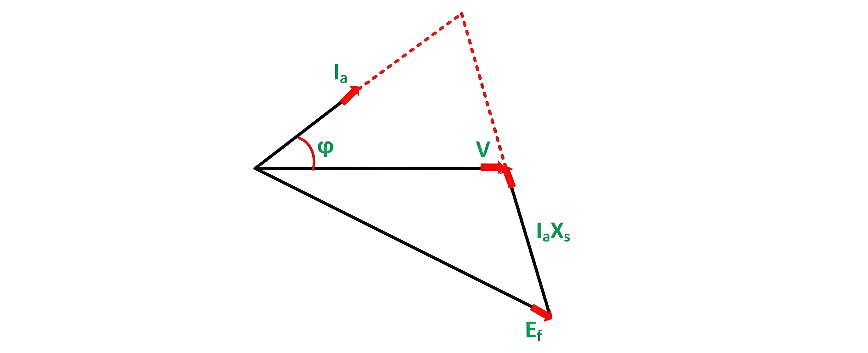
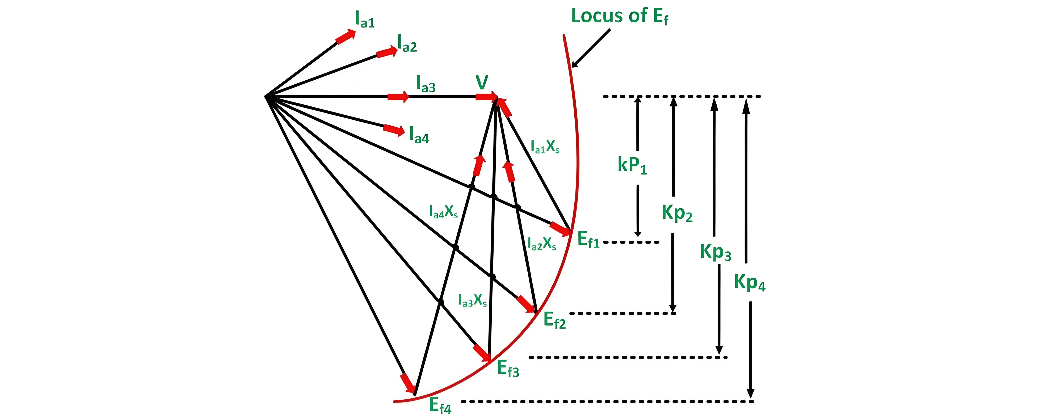
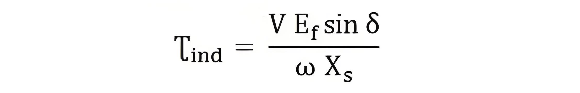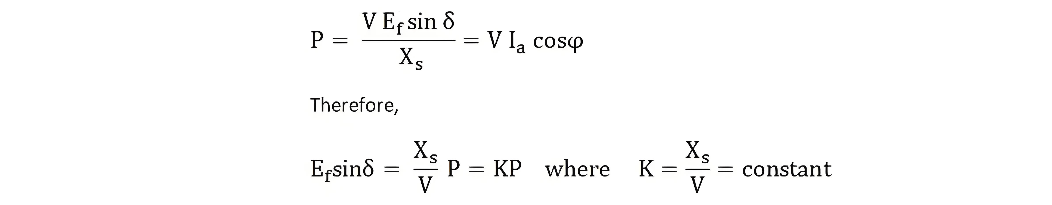As depicted in the figure above, as the load increases, the quantity jIaXs steadily grows, and the equation V=Ef+jIaXs

remains valid. Concurrently, the armature current also rises. The power factor angle undergoes a transformation with the load variation; it gradually becomes less leading and then increasingly lagging, as clearly illustrated in the figure.

In summary, when the load on a synchronous motor increases, the following key observations can be made:

The motor maintains its operation at the synchronous speed.
The torque angle δ expands.
The excitation voltage Ef stays constant.
The armature current Ia drawn from the power supply increases.
The phase angle ϕ shifts further in the lagging direction.

It's important to note that there is a limit to the mechanical load that a synchronous motor can handle. As the load continues to rise, the torque angle δ keeps increasing until a critical point is reached. At this juncture, the rotor is pulled out of synchronism, causing the motor to come to a halt.

The pull - out torque is defined as the maximum torque that a synchronous motor can generate at the rated voltage and frequency while still maintaining synchronism. Typically, its values range from 1.5 to 3.5 times the full - load torque.